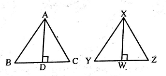TS Polycet (Polytechnic) 2015 Previous Question Paper with Answers And Model Papers With Complete Analysis

4271 total views , 4 views today

Q). The equation of the line passing through (0, 0) and (a cosα, b sinα) is
A) ay – bx tan α
B) by = ax tan α
C) by = – ax tan α
D) ay = – bx tan α

View Answer

A) ay – bx tan α
Explanation: Let A(0, 0), B(a cos a, b sin a)
The equation of $\overline{AB}$

is
Y – y₁ = $\frac{Y_2-Y_1}{X_2-X_1}(X-X_1)$

Y – 0 = $\frac{b\;\sin\alpha-0}{a\;\cos\alpha-0}(X-0)$

Y = $\frac{b\;\sin\alpha}{a\;\cos\alpha}X$

⇒Y = b/a tanα x⇒ ay = bx tanα

Q). The area of the triangle formed by (a, b + c), (b, c + a) and (c, a + b) is
A) a + b + c sq. units
B) abc sq. units
C) (a + b + c)² sq. units
D) 0 sq. units

View Answer

D) 0 sq. units
Explanation: Bet A(a, b + c), B(b, c + a), c(c, a + b)
The area of the triangle ΔABC
= $\frac12\begin{vmatrix}X_1-X_2&Y_1-Y_2\\X_1-X_3&Y_1-Y_3\end{vmatrix}$

= $\frac12\begin{vmatrix}a-b&b+c-c-a\\a-c&b+c-a-b\end{vmatrix}$

= $\frac12\begin{vmatrix}a-b&b-a\\a-c&c-a\end{vmatrix}$

= $\frac12\left|(a-b)\;(c-a)-(b-a)(a-c)\right|$

= $\frac12\left|\cancel{ac}-\cancel{a^2}-\cancel{bc}+\cancel{ab}-\cancel{ab}+\cancel{bc}+\cancel{a^2}-\cancel{ac}\right|$

Q). The nearest point from the origin is
A) (2, -1)
B) (3, -1)
C) (5, 0)
D) (2, -3)

View Answer

A) (2, -1)
Explanation: Verify options O (0, 0)
1) O (0,0), (2,-1) ⇒ $\sqrt{4+1}$

= √5
2) O (0,0), (3,-1) ⇒ $\sqrt{9+1}$

=√10
3) O (0, 0), (5, 0) ⇒ $\sqrt{25+0}$

=√25
4) O (0, 0), (2, -3) ⇒ $\sqrt{4+9}$

=√13

Q). If the points (a, 0), (0, b) and (1, 1) are collinear, then $\frac1a+\frac1b$ =
A) -1
B) 2
C) 0
D) 1

View Answer

D) 1
Explanation: Let A (a, 0), B (0, b), C(1, 1)
Slope of $\overline{AB}$

= slope of $\overline{BC}$

⇒ $\frac{b-0}{0-a}=\frac{1-b}{1-0}\Rightarrow\frac b{-a}=\frac{1-b}1\Rightarrow\frac{-b}a=1-b$

⇒ $\frac1b+\frac1a=1$

∴ $\frac1a+\frac1b=1$

Q). The equation of a straight line passing through the points (4, -7) and (1, -5) is
A) 2x + 3y-13 = 0
B) 2x-3y+ 13 = 0
C) 2x + 3y+13 = 0
D) 2x-3y-13 = 0

View Answer

C) 2x + 3y+13 = 0
Explanation: Let A(4,-7), B (1, – 5) Equation of $\overline{AB}$

is $Y-Y_1\;=\frac{Y_2-Y_1}{X_2-X_1}(X-X_1)$

$Y+7\;=\frac{-5+7}{1-4}(X-4)$

Y+7 = 2/3 (x-4)
-3y-21 = 2x-8
⇒2x+3y+13 = 0

Q). The slope of the line which is parallel to 3x – 2y + 1 = 0 is
A) -3/2
B) 3/2
C) 2/3
D) -2/3

View Answer

B) 3/2
Explanation: Slope of the line 3x – 2y + 1 = 0 is
M = -a/b = -3/-2 = 3/2
Slope of the parallel line = m = 3/2

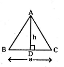
Q). In an equilateral triangle ABC if AD ⊥ BC, then AD²=
A) 2CD²
B) 3 CD²
C) 4 CD²
D) 5 CD²

View Answer

B) 3 CD²
Explanation: ΔABC, is an equilateral triangle, AD-height and side ‘a’ units.
Height h units

In ΔABD, ΔACD
∠B = ∠C (∴60°)
∠ADB = ∠ADC (∴90°)
∠BAD = ∠DAC
(∴Sum of the angles property) and BA = CA.
∴∠ABD = ∠ACD (∴SAS congruence condition)
BD = CD = 1/2 BC = a/2 (∴ C.P.C.T.)
ΔABD, AB² = AD² + BD² (∴Pythagoras theorem)
A² = h² +(a/2)² a² = h² +a²/4
h² = 4a²-a²/4 = 3a²/4
⇒4h² = 3a² ⇒ 4(AD)² = 3(BC)²
⇒ 4(AD)² = 3(2 CD)²
⇒ 4(AD)² = 3 x 4 CD²
⇒ 4(AD)² = 12 CD²
⇒ (AD)² = 12CD²/4 = 3CD²

Q). The areas of two similar triangles are 121 cm² and 64 cm² respectively. If the median of the first triangle is. 12.1 cm, then the corresponding median of the other triangle is
A) 11 cm
B) 8.1 cm
C) 11.1 cm
D) 8.8 cm

View Answer

D) 8.8 cm
Explanation:

ΔABC/ΔXYZ = AD²/XW²
121/64 = (12.1)²/XW² ⇒121/64 = 146.41/XW²
XW² = 146.4×64/121 = 77.44
XW = √77.44 = 8.8 cm

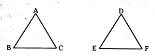
Q). If in two triangles ABC and DEF, $\frac{AB}{DE}=\frac{BC}{FE}=\frac{CA}{FD}$ , then
A) ΔFDE ~ ΔCAB
B) ΔFDE ~ ΔABC
C) ΔBCA ~ ΔFDE
D) None

View Answer

C) ΔBCA ~ ΔFDE
Explanation:

$\frac{AB}{DE}=\frac{BC}{FE}=\frac{CA}{FD}$

⇒ ΔBCA ∼ ΔFDE

Q). If the ratio of perimeters of two similar triangles is 9 : 16, then the ratio of their altitudes is
A) 16 : 9
B) 3 : 4
C) 9 : 16
D) 4 : 3

View Answer

C) 9 : 16
Explanation: P₁/h₁ ⇒ 9/16= h₁/h₂
H₁/h₂ =9:16

Spread the love

Pages: 1 2 3 4 5 6 7 8 9 10 11 12

Leave a Reply Cancel reply