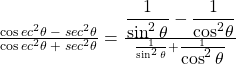TS Polycet (Polytechnic) 2015 Previous Question Paper with Answers And Model Papers With Complete Analysis

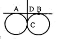
Q). In a rhombus, the diagonals intersect at
A) 120°
B) 100°
C) 80°
D) 90°

View Answer

D) 90°
Explanation: 90°

Q). Find the area of the shaded region in the figure, if ABCD is a square of side 7 cm, and APD and BPC are semicircles. (Take π = 22/7)

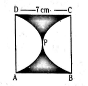
A) 12.5 cm²
B) 10.5 cm²
C) 11.5 cm²
D) 9.5 cm²

View Answer

B) 10.5 cm²
Explanation: Given, ABCD is a square of side 7 cm.
Area of the shaded region
= Area of ABCD – Area of two
semi circles with radius 7/2 = 3.5 cm
APD and BPC are semi circles
=7×7-2×1/2×22/7×3.5×3.5
= 49-38.5 = 10.5 cm²
∴ Area of shaded region=10.5 cm²

Q). AB and CD are two common tangents to circles which touch each other at C. If D lies on AB such that CD = 4 cm, then AB is equal to
A) 4 cm
B) 6 cm
C) 8 cm
D) 12 cm

View Answer

C) 8 cm
Explanation: CD = 4 cm
∴AD = BD = CD
∴AB = AD + BD

= 4 + 4 = 8 cm

Q). If tangents PA and PB from a point P to a circle with centre O are inclined to each other at angle of 80°, then ∠POA is equal to
A) 60°
B) 45°
C) 30°
D) 50°

View Answer

D) 50°
Explanation:
If ∠APB = 80°
then ∠AOB = 180° – 80° = 100°
∠POA = 180° – (40° + 90°)
= 180°-130° = 50°

Q). In the figure given below, AP is a tangent to the circle with centre O such that. OP = 4 cm and ∠OPA = 30°, then AP =

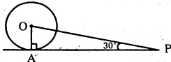
A) 2√2 cm
B) 2 cm
C) 2√3 cm
D) 3√2 cm

View Answer

C) 2√3 cm
Explanation:
In ΔOPA
cos 30° = PA/OP
⇒√3/2 = PA/4 ⇒PA = 2√3 cm

Q). The angle in a semicircle is
A) 90°
B) 180°
C) 360°
D) 270°

View Answer

A) 90°
Explanation: The angle in a semi circle is 90°

Q). The volume of a cylinder is 49896 cm3 and its curved surface area is 4752 sq. cm, then its radius is
A) 12.3 cm
B) 21 cm
C) 10 cm
D) 13.7 cm

View Answer

B) 21 cm
Explanation: In cylinder volume = 49896 cm³
πr²h = 49896 ………………………(1)
Curved surface Area = 4752 sq.cm.
2πrh = 4752 ………. (2)
Now (1)/(2) ⇒ πr²h/ 2πrh =49896/4752
r/2 = 10.5 ⇒ r =21 cm

Q). A cylindrical pencil is sharpened to produce a perfect cone at one end with no overall loss of its length. The diameter of the pencil is 1 cm and the length of the conical portion is 2 cm. Calculate the volume of the shavings. (Take, π = 355/113)
A) 0.05 cm³
B) 1.5 cm³
C) 0.5 cm³
D) 1.05 cm³

View Answer

D) 1.05 cm³
Explanation: Diameter of the pencil = 1 cm.
So, radius of the pencil r = 0.5 cm
Length of the conical portion = 2 cm.
Volume of shavings = Volume of cylinder of the length 2 cm and base radius 0.5 cm – Volume of the cone formed by this cylinder.
= π r²h – 1/3 π r²h
= 2/3 π r²h
= 2/3 x355/113 x (0.5)² x²
= 1.05 cm³

Q). If the diagonals of a rhombus are 10 cm and 24 cm, then the area is
A) 200 cm²
B) 120 cm²
C) 240 cm²
D) 20 cm²

View Answer

B) 120 cm²
Explanation: d₁ = 10 cm
D₂ = 24 cm
Area = 1/2 d₁ d₂= 1/2 x10x24
= 120 cm²

Q). If tanθ = 1/√7, then $\frac{\cos ec^2\theta\;-\;sec^2\theta}{\cos ec^2\theta\;+\;sec^2\theta}$ =
A) 5/7
B) 3/7
C) 1/12
D) 3/4

View Answer

D) 3/4
Explanation: tanθ = 1/√7
$\frac{\cos ec^2\theta\;-\;sec^2\theta}{\cos ec^2\theta\;+\;sec^2\theta} = \frac{\displaystyle\frac1{\sin^2\theta}-\frac1{{\displaystyle\cos}^2\theta}}{\frac1{\sin^2\theta}+\frac1{\textstyle\cos^2\theta}}$

= $\frac{\cos^2\theta\;-\;\sin^2\theta}{\cos^2\theta\;+\;\sin^2\theta}$

= cos2θ/1 = cos2θ = $\frac{1\;-\;\tan^2\theta}{1\;+\;\tan^2\theta}$

= $\frac{1\;-\;{\displaystyle\frac17}}{1\;+\;{\displaystyle\frac17}}$

= $\frac{\displaystyle\frac{7-1}7}{\displaystyle\frac{7+1}7}$

= 6/8
= 3/4

Spread the love

Leave a Comment Cancel reply