4272 total views , 5 views today

Q). If n is a natural number, then 6 ⁿ – 5ⁿ always ends with
A) 7
B) 5
C) 3
D) 1

Q). If n(A) = 5, n(B) = 5 and n(A ∪ B) = 8, then n(A ∩ B) =
A) 2
B) 3
C) 1
D) None

Q). If A = {x/x ∈ N, I < x < 10}, then n(A) =
A) 3
B) 4
C) 8
D) None

Q). Identify the disjoint sets among the following:
A) A-B, B-A
B) A-B, A
C) B-A, B
D) None

Q). If two zeroes of the polynomial x³ + 3 x² – 5x – 15 are √5 and – √5, then its third zero is
A) 3
B) 5
C) -3
D) -5

Q). If α and β are the zeroes of the polynomial f(x) = a x² + bx +c, then 1/α + 1/β =
A) b/c
B) –b/c
C) c/b
D) –c/b

View Answer

B) –b/c
Explanation: α+β = -b/a , αβ = c/a
1/α + 1/β = α+β/αβ = = -b/c

Q). If the diagram shows the graph of the polynomial f(x) = a x² + bx + c, then

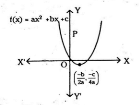
A) a > 0, b < 0 and c > 0
B) a < 0, b < 0 and c < 0
C) a < 0, b > 0 and c > 0
D) a < 0, b > 0 and c < 0

Q). If x = 2 + 2^2/3 + 2^1/3, then the value of x³ – 6 x² + 6x =
A) 3
B) 1
C) 2
D) -2

Q). If am ≠ bl, then the system of equations ax + by = c, lx + my = n
A) has a unique solution
B) has no solution
C) has infinitely many solutions
D) has two solutions

Q). The area of the triangle formed by the lines y = x, x = 6 and y = 0 is
A) 36 sq. units
B) 72 sq. units
C) 9 sq. units
D) 18 sq. units

View Answer

D) 18 sq. units
Explanation: y = x …. (1), x = 6………..(2) , y = 0…………..(3)

(1), (3) ⇒ A(0,0)
(1), (2) ⇒B(6, 6)
(2) ,(3) ⇒C(6,0)
Area =
=
=
= = 36/2 = 18