Q). In an isosceles triangle ABC with AC = BC if AB2 = 2AC2, then ∠C =
A) 30°
B) 90°
C) 45°
D) 60°
Q). In a right-angled triangle ABC right-angled at B. If P and Q are points on the sides AB and BC respectively, then which of the following is true?
A) AQ2 + CP2 = 2(AC2 + PQ2)
B) 2(AQ2 + CP2) = AC2 + PQ2
C) AQ2 + CP2 = AC2 + PQ2
D) None
Q). In △ABC the sides are 6, 10 and 8, then △ABC is
A) Right-angled triangle
B) Acute angled triangle
C) Obtuse angled triangle
D) None
Q). From the given figure, value of OP is
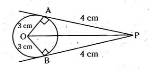
A) 5
B) 4
C) √8
D) 3
Q). The angle between a tangent to a circle and the radius at the point of contact is
A) 60°
B) 30°
C) 45°
D) 90°
Q). If two circles touch each other internally, then how many common tangents can be drawn?
A) 5
B) 4
C) 0
D) 1
Q). Number of parallel tangents to a circle with a given tangent is
A) 1
B) 2
C) 4
D) 3
Q). In the figure, area of the segment PAQ is ……………. sq. units.
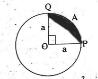
A) ![\frac{a2}4\left[\pi+2\right]](https://www.mcqbits.com/wp-content/ql-cache/quicklatex.com-b0f7ae172a93fde55cc2ac43559a2e65_l3.png "Rendered by QuickLaTeX.com")
B) ![\frac{a2}4\left[\pi-2\right]](https://www.mcqbits.com/wp-content/ql-cache/quicklatex.com-c482a8560d27a08c8ceb438ab5289fc9_l3.png "Rendered by QuickLaTeX.com")
C) ![\frac{a2}4\left[\pi-1\right]](https://www.mcqbits.com/wp-content/ql-cache/quicklatex.com-c940f20b56b6dcefa9738942ba62e76a_l3.png "Rendered by QuickLaTeX.com")
D) ![\frac{a2}4\left[\pi+1\right]](https://www.mcqbits.com/wp-content/ql-cache/quicklatex.com-84c4eea51642f1f13f100a521b97509e_l3.png "Rendered by QuickLaTeX.com")
Explanation: Area of the segment PAQ
= Area of sector—Area of triangle
=
=
=
Q). In the below figure, if PT = 6 cm, PA = 3 cm, then AB equals to
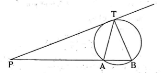
A) 2 cm
B) 9 cm
C) 5 cm
D) 6 cm
Q). The volume of a vessel in the form of cylinder is 448π cm3 and its height is 7 cm, then the radius of the base is
A) 2 cm
B) 8 cm
C) 6 cm
D) 4 cm